[コンプリート！] 3 元 2 次 連立 方程式 解き方 278961

2年2章 連立方程式の解き方 Math Connect 東京書籍 先生のための算数数学ポータルサイト

 未知数が3つになったら3元1次方程式と言います。 この記事では特に2元1次連立方程式の解説をしていきます。 このあたりの用語が怪しい人は、「 解説を読んでもわからない 」という失敗に繋がる危険性が高いので、教科書を見てしっかり確認しましょう。 連立方程式を解くためのアイデアは， 変数を消去する ということに尽きます．何らかの方法で，変数を消去していき，たったひとつの変数のみの式を作り出せれば解くことができるわけです． 連立 2 2 元 1 1 次方程式の解き方は大きくわけて 2 2 つあります

3 元 2 次 連立 方程式 解き方

3 元 2 次 連立 方程式 解き方- 3つの式がつながっている方程式の解き方 2 3つの式、文字がある連立方程式の解き方 21 手順① 1つの文字を消し、2つの文字の連立方程式を作る 22 手順② 手順①で作った連立方程式から2つの文字の値を求める 23 手順③ 残り1つの文字の値を求める解き方をみわける2つのコツ 連立方程式の解き方の 割は「加減法」！

連立方程式の2つの解き方 代入法 加減法 数学fun

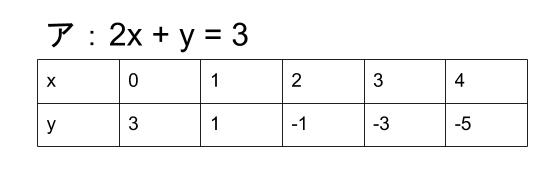
 2元1次方程式のグラフの書き方がわからないんですが教えていただけますか？ (3) 解をもたない 2 元連立一次方程式（2 変数の連立一次方程式）の例を 1 小数と分数をふくむ一次方程式の解き方 ;難しくはありません！ 式が2つあるだけです (正確には、ここでは二元一次方程式が2つあるだけです) 先に軽くふれましたが、文字が2種類なら、等式が2つあれば、 解が1つに決まる というものですね。 では解き方です 《 例 》 次の連立方程式を解き解の公式を用いて次の2次方程式を解きなさい。 次に平方完成で解き，解き方を比較しなさい。 （1） x 2 ＋3 x ＋1＝0 （2） x 2 ＋2 x －6＝0

 連立方程式の解き方（加減法or代入法）をみわけるコツ を紹介していくよ。 すっきりしたいときに参考にしてみて^^ 〜もくじ〜 解き方を勉強する前に知っておきたいこと; 連立方程式「a=b=c」の解き方 次の方程式を解きなさい。 3つの式がつながっているときには、まず3つのうち2つを選んで式を作ります。 さっきとは違うペアでもう1つ式を作ります。 すると、2つ式ができたことになりますね。 ここから連立方程式を作り3つの文字、式の連立方程式を解くためには まず、文字を1つ消してやることがポイントでしたね！ そうすることで今まで解いてきた連立方程式と同じ形を作ることができます。 たくさん練習して、しっかりと手順を身につけておこうね (^^) ファイトだー

3 元 2 次 連立 方程式 解き方のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
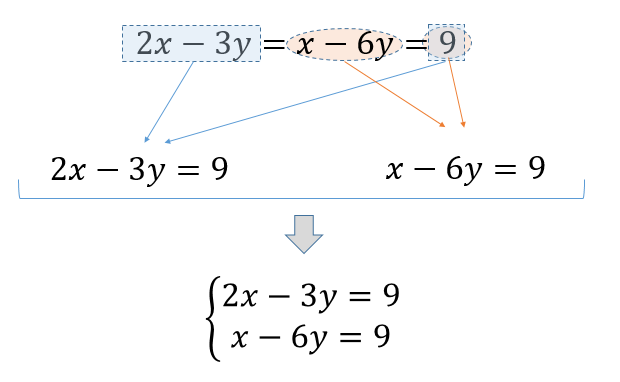高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	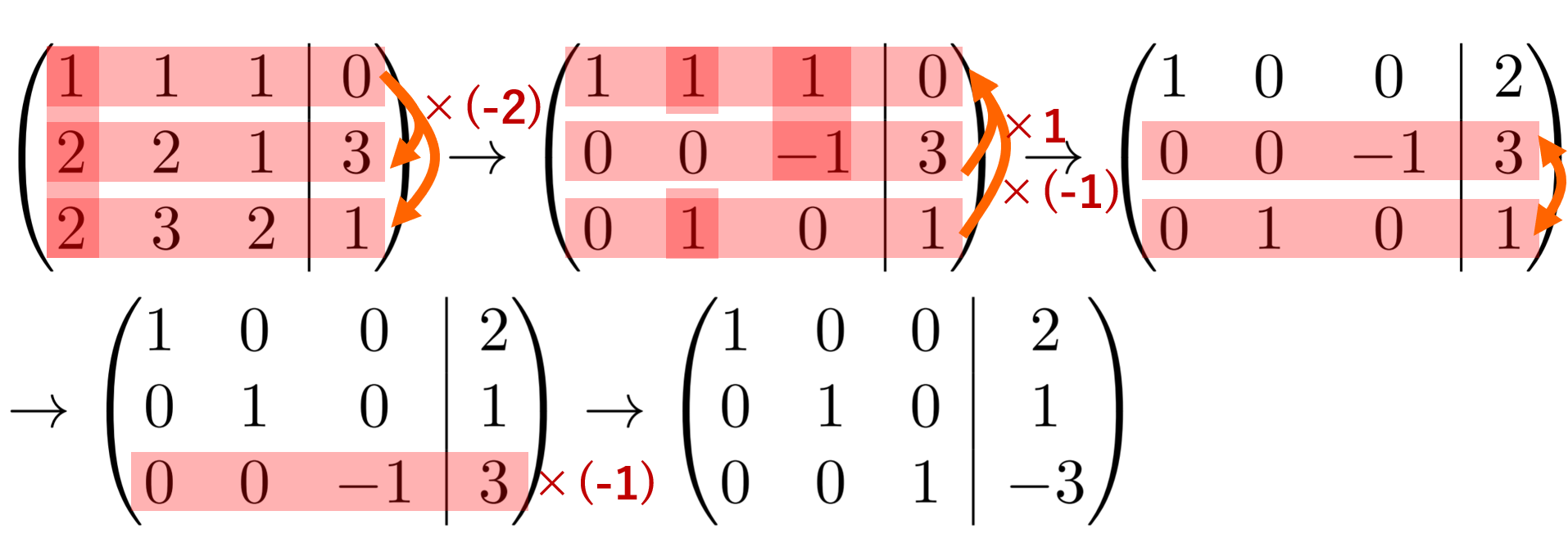高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
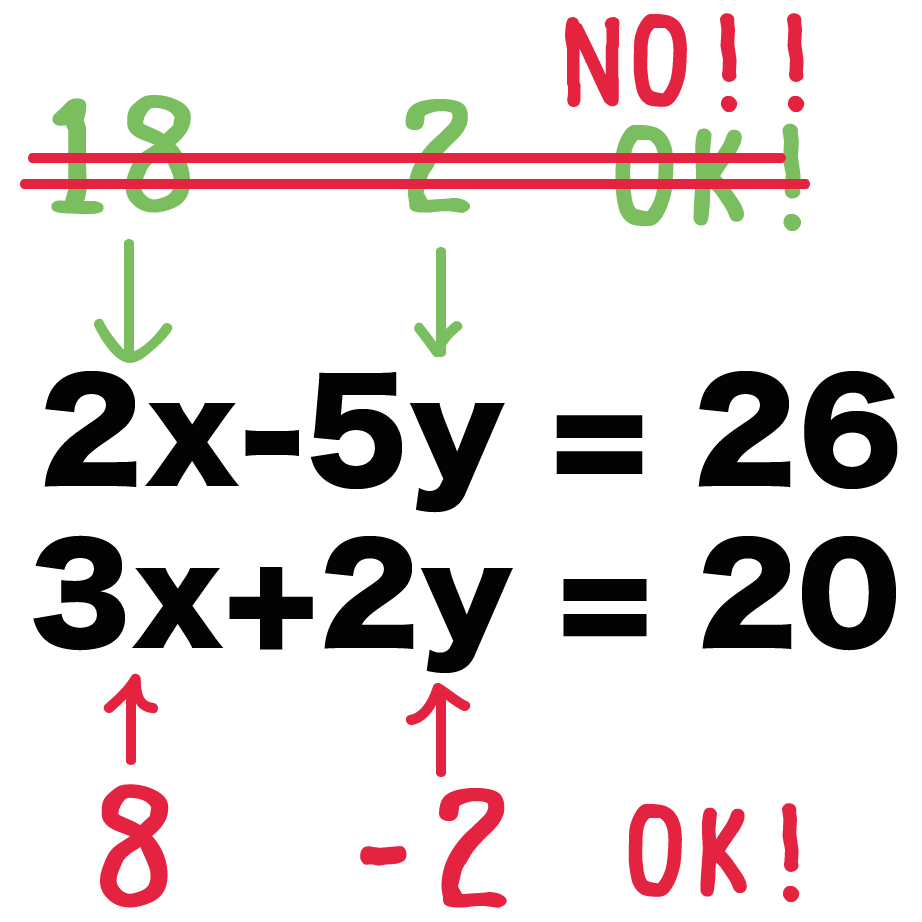高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	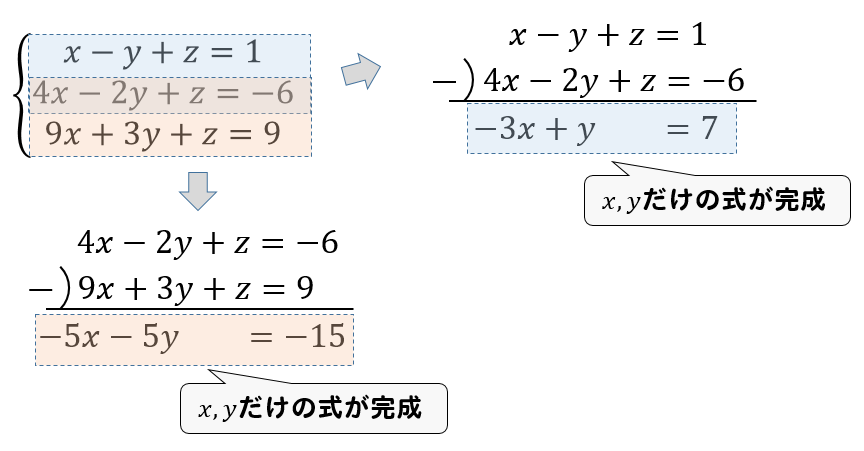高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	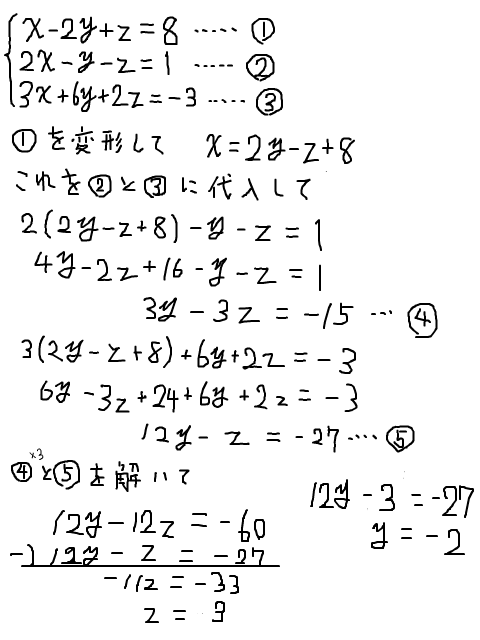高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ

何度も繰り返し練習しましょう！ それが成績アップのコツですよ。 「なぜ」2つの解き方を習うの？ 中2で学習する 「連立方程式」 は、 加減法、代入法のどちらでも 同じ答えになります。 こう説明すると、 "ではなぜ、2つの解き方を習うの？ " 行列を使った解き方 の二つを見ていきましょう。 11 普通の解き方 通常の方法では、この連立方程式を解くには、まず以下のように「 ( 2) − 2 × ( 1) 」 を行うことで y の値を得ます。 2 x 4 y = 22 −) ( 2 x 2 y = 18) =) 2 y = 4 =) y = 2 これで y = 2 であることが